CRYPTO

作者：xinyi

RSA

对称加密

最初（1）甲方选择某一种加密规则，对信息进行加密；
（2）乙方使用同一种规则，对信息进行解密。
这就有了缺点甲方必须要把加密规则告诉乙方，否则无法解密。但是这样安全性就没有办法保证了，传输过程中可能会被拦截这样就导致信息传输不安全。

非对称加密（RSA,ECC,DSA等）

1、消息接收方准备好公钥和私钥
2、私钥接收方自己留存、公钥发布给消息发送方
3、消息发送方使用接收方公钥对消息进行加密
4、消息接收方用自己的私钥对消息解密

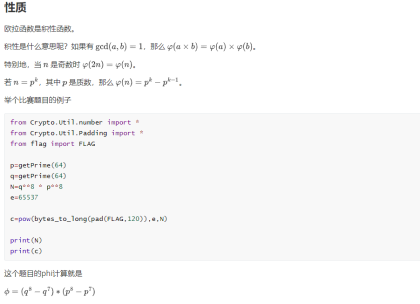
RSA加密解密

第一步，随机选择两个不相等的质数p和q。

爱丽丝选择了61和53。（实际应用中，这两个质数越大，就越难破解。）

第二步，计算p和q的乘积n。

爱丽丝就把61和53相乘。

n = 61×53 = 3233

n的长度就是密钥长度。3233写成二进制是110010100001，一共有12位，所以这个密钥就是12位。实际应用中，RSA密钥一般是1024位，重要场合则为2048位。

第三步，计算n的欧拉函数φ(n)。

n是质数，则 φ(n)=n-1
n = p1 × p2
φ(n) = φ(p1p2) = φ(p1)φ(p2)
=> φ(n) = (p-1)(q-1)

爱丽丝算出φ(3233)等于60×52，即3120。

第四步，随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质。

爱丽丝就在1到3120之间，随机选择了17。（实际应用中，常常选择65537。）

第五步，计算e对于φ(n)的模反元素d。

所谓”模反元素”就是指有一个整数d，可以使得ed被φ(n)除的余数为1。

ed ≡ 1 (mod φ(n))

这个式子等价于

ed - 1 = kφ(n)

于是，找到模反元素d，实质上就是对下面这个二元一次方程求解。(-k = y)

ex + φ(n)y = 1

已知 e=17, φ(n)=3120，

17x + 3120y = 1

这个方程可以用扩展欧几里得求解，爱丽丝算出一组整数解为 (x,y)=(2753,-15)，即 d=2753。

至此所有计算完成。

离散对数

不知道为什么网站用不了数学符号然后就直接全部截图了。

在一次数学联考时候遇到了离散对数

有亿点点恶心这个题，给的符号ⓧ就是mod直接写成mod p何必要这么麻烦。
然后就想到学一学离散对数了。
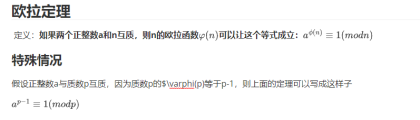
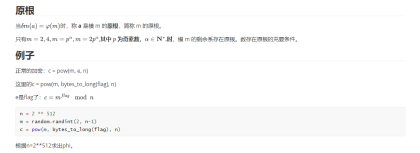
前置知识:欧拉定理 & 费马小定理
同余方程

离散对数

---

• 分类： CTF学习
• 标签： CRYPTO